2012년04월07일 8번
[과목 구분 없음] 그림과 같은 콘크리트로 된 기둥(단주)에 하중 P가 도심에 작용하여 A부분에 압축응력 fA=5MPa, B부분에 압축응력 fB=3MPa가 각 부재에 일정하게 발생하였다. 이들 응력을 5년 이상의 장기 하중으로 받을 때, 탄성변형 및 크리프 변형에 의한 총 압축변위 [mm]는? (단, 콘크리트의 설계기준강도 fck=19MPa, 크리프 계산을 위한 콘크리트의 탄성계수 Ec=2.5 × 104MPa, 자중은 무시하며, 기둥은 옥외에 있다)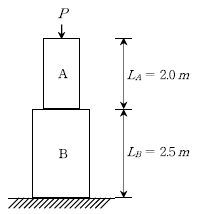

- ① 1.5
- ② 1.8
- ③ 2.1
- ④ 2.4
(정답률: 10%)
문제 해설
총 압축변위는 탄성변형과 크리프 변형의 합으로 구할 수 있다.
탄성변형에 의한 압축변위는 다음과 같이 구할 수 있다.
Δelastic = P/(A×Ec)×(1-ν2)×(hA/2+hB/2)
여기서 A는 단면적, Ec는 콘크리트의 탄성계수, ν는 포아송비, hA와 hB는 각각 A와 B부분의 높이이다.
따라서 Δelastic = 100/(π×0.32×2.5×104)×(1-0.22)×(1.5/2+3/2) ≈ 0.36mm
크리프 변형에 의한 압축변위는 다음과 같이 구할 수 있다.
Δcreep = α×P×t0/A
여기서 α는 크리프계수, t0은 하중을 받기 시작한 시점부터의 시간이다.
크리프계수는 다음과 같이 구할 수 있다.
α = 0.7×fck1/3/Ec
따라서 α ≈ 2.2×10-6
5년 이상의 장기 하중을 받을 때 t0 = 5×365×24×60×60 ≈ 157680000초이다.
따라서 Δcreep = 2.2×10-6×100×157680000/(π×0.32) ≈ 1.74mm
따라서 총 압축변위는 Δelastic + Δcreep ≈ 0.36 + 1.74 ≈ 2.1mm 이다.
따라서 정답은 "2.1"이다.
탄성변형에 의한 압축변위는 다음과 같이 구할 수 있다.
Δelastic = P/(A×Ec)×(1-ν2)×(hA/2+hB/2)
여기서 A는 단면적, Ec는 콘크리트의 탄성계수, ν는 포아송비, hA와 hB는 각각 A와 B부분의 높이이다.
따라서 Δelastic = 100/(π×0.32×2.5×104)×(1-0.22)×(1.5/2+3/2) ≈ 0.36mm
크리프 변형에 의한 압축변위는 다음과 같이 구할 수 있다.
Δcreep = α×P×t0/A
여기서 α는 크리프계수, t0은 하중을 받기 시작한 시점부터의 시간이다.
크리프계수는 다음과 같이 구할 수 있다.
α = 0.7×fck1/3/Ec
따라서 α ≈ 2.2×10-6
5년 이상의 장기 하중을 받을 때 t0 = 5×365×24×60×60 ≈ 157680000초이다.
따라서 Δcreep = 2.2×10-6×100×157680000/(π×0.32) ≈ 1.74mm
따라서 총 압축변위는 Δelastic + Δcreep ≈ 0.36 + 1.74 ≈ 2.1mm 이다.
따라서 정답은 "2.1"이다.



